简单的 GWAS 教程

假设有这样一个控制粒宽的 SNP，在一个 300 个品种的群体中，如果一个品种在这个位点是 C，它的粒宽就相对较窄的，是 G 的话则相对较宽。

如果我们对这 300 个品种的粒宽性状进行测量，同时也测定它们在这个 SNP 上的基因型，将 300 个品种分成 C 和 G 两组，用 T-test 检验粒宽上的差异，那么所得到的 P 值肯定会是一个很小的数字。

然而现实情况是，我们并不知道这样的控制粒宽的 SNP 在哪。我们所拥有的，是在这 300 个品种的基因组上有 1000000 个 SNP 位点，通过测序，我们得到了 300 个品种的的基因型数据，同时通过测量种子，得到了这 300 个品种的粒宽的表型统计数据。

如何寻找控制粒宽的 SNP 呢？一个最简单的方法就是像上面那样做 T 检验，做上一百万次，SNP 的 P 值越小，它就越可能是我们想找的。

这就是一个最简化的全基因组关联分析（GWAS），一种通过将基因型数据与表型数据进行关联分析，进而从中寻找与表型相关联的基因组区间，甚至定位相关基因的分析方法。当然，实际的 GWAS 的计算过程比这要复杂得多。

本文将利用 3K-RG 测序计划的基因型数据，以及公开的表型数据，做一个简单的 GWAS。

本文所用到的脚本已上传至配套的 Github 仓库

准备工作

获取基因型数据

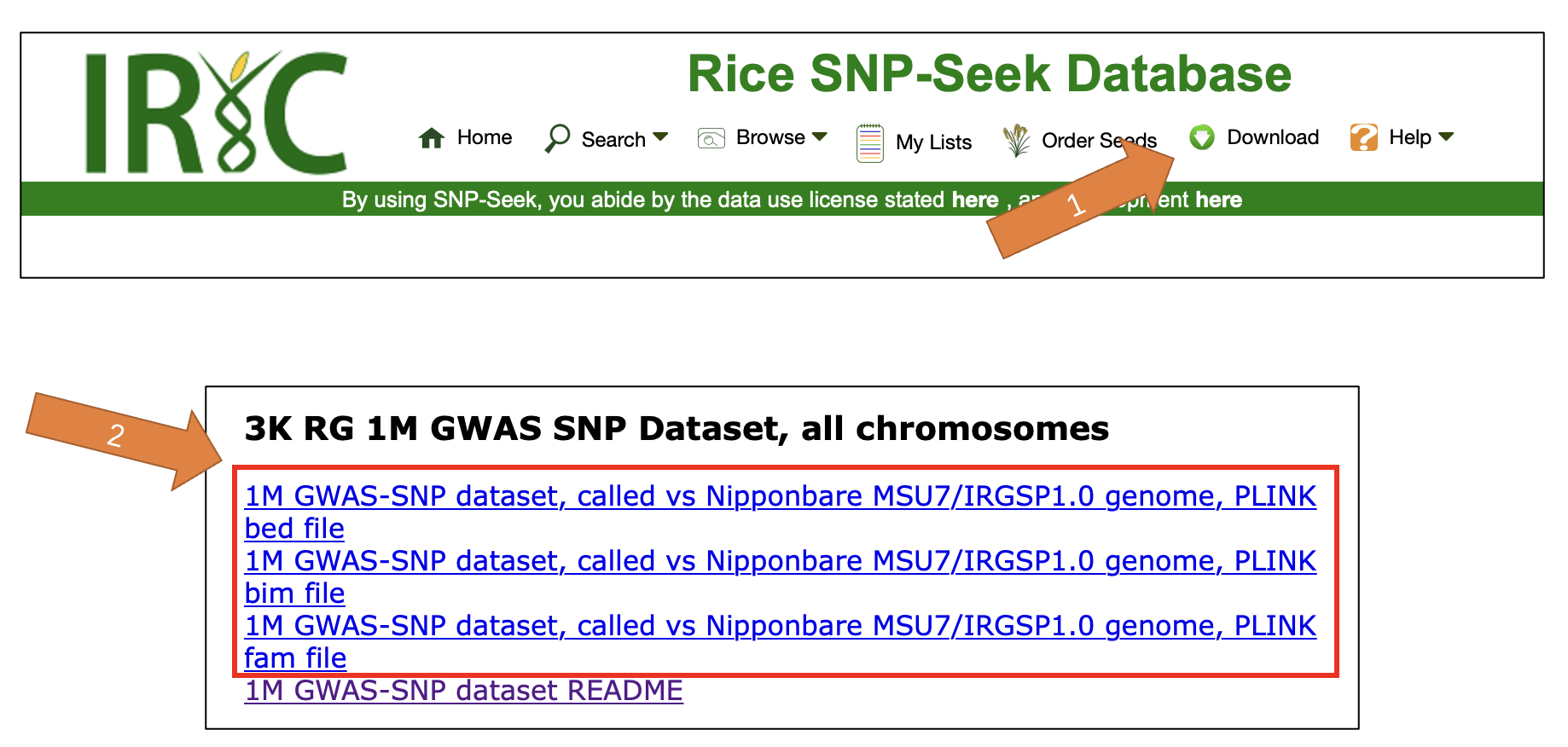
基因型数据可从国际水稻所的 SNP-Seek 数据库下载，这里我们下载 “3K RG 1M GWAS SNP Dataset, all chromosomes” 下的数据，这是 PLINK-BED 格式的数据，三个文件为一组数据，应始终放在一起。

二进制的 bed 文件存放着具体的每个品种的每个 SNP 位点是什么基因型这样的信息
纯文本的 fam 文件中存放着品种的编号和表型等信息（下载的 fam 文件里只有编号，表型数据是缺失值）
纯文本的 bim 文件中存放着 SNP 的物理位置等信息

有关 PLINK 格式的详细信息，可参考 PLINK 的文档。

download-from-snp-seek

获取表型数据

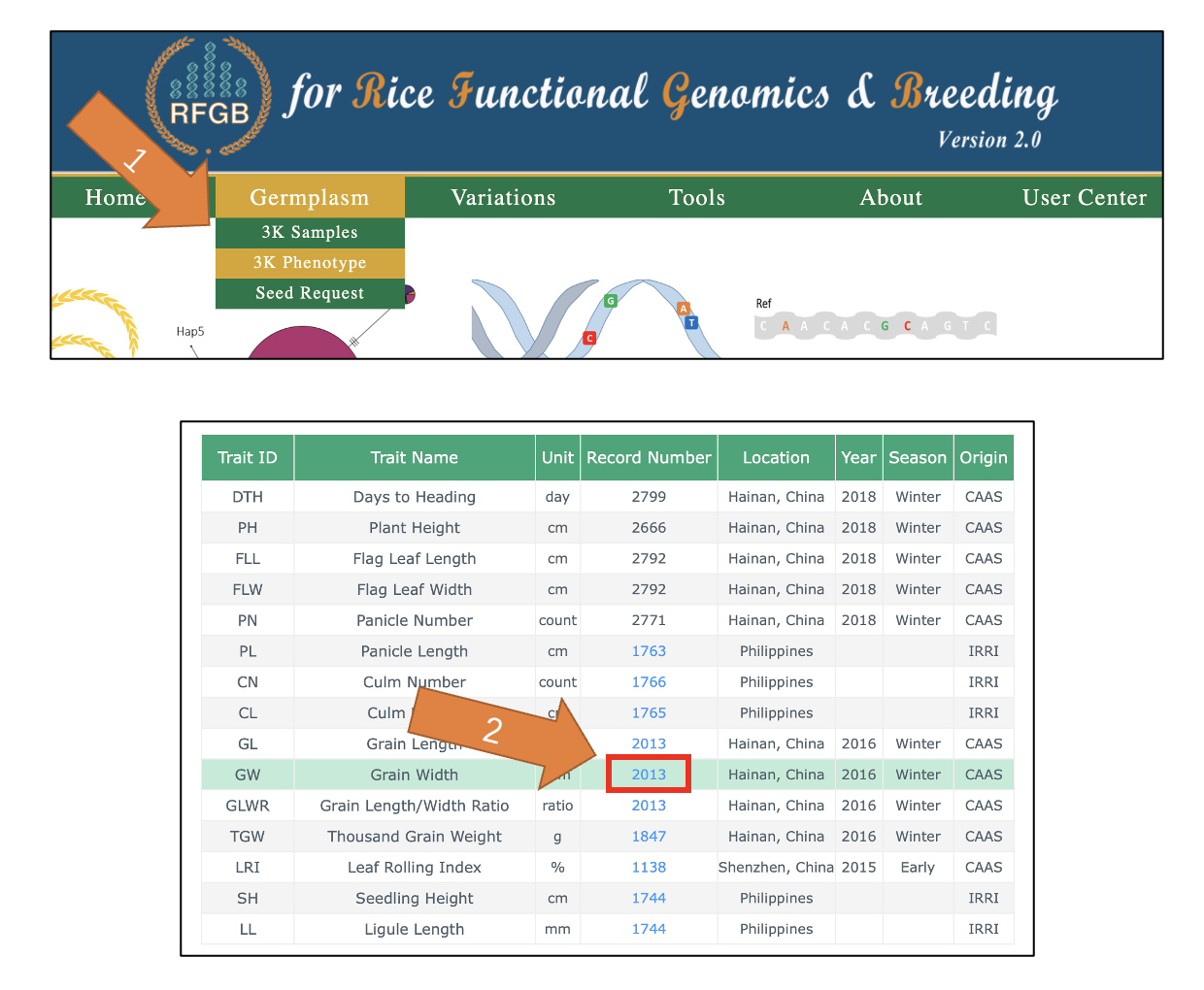
表型数据可从 RFGB 数据库下载。这里我们选择下载粒宽的数据。

download-from-rfgb

安装软件

通过 conda 可快速安装需要的软件。首先将下面的 YAML 复制进一个文本文件中（比如 env.yaml）。

name: gwas
channels:
  - bioconda
  - conda-forge
dependencies:
  - plink=1.90
  - r-base=4.1
  - r-tidyverse
  - gemma
  - r-qqman

然后通过下面的命令即可创建一个装好需要的软件的环境。

conda env create --file env.yaml

通过 conda activate gwas 即可激活环境。

建立项目文件夹

养成良好的习惯，创建一个项目文件夹，将下载下来的文件都放进来，形成如下所示的目录结构。

.
├── env.yaml
├── rawdata
│   ├── grain_width.zip
│   ├── pruned_v2.1.bed
│   ├── pruned_v2.1.bim
│   └── pruned_v2.1.fam
├── resources
├── results
└── scripts

分析流程

数据预处理

3K-RG 测序计划测了 3000+ 个品种，下载的粒宽表型数据也有 2000+ 个品种的数据，作为一个教程，数据太大用个人电脑跑起来会很吃力，所以让我们随机地选出 300 个品种。

先用 R 语言脚本读入表型数据，并随机地挑出 300 个品种及其对应的表型数据，这将生成一个格式与之前下载好的 fam 文件一样的文件：resources/selected.fam。

library(tidyverse)

grain_width <- read_tsv(
    "rawdata/grain_width.zip",
    col_names = c("ID", "Value")
)

set.seed(1)

selected_fam <- grain_width %>%
    slice_sample(n = 300) %>%
    transmute(FID = ID, IID = ID, Father = 0, Mother = 0, Sex = 0,  Value)

write_delim(selected_fam, "resources/selected.fam", col_names = F, delim = " ")

然后，用 PLINK 以刚才生成的 fam 文件为名单，从下载下来的总的 PLINK-BED 格式数据中，将 300 个品种的基因型信息提取出来，生成新的一组数据：resources/gwas.bed， resources/gwas.bim 和 resources/gwas.fam。

plink \
    --keep resources/selected.fam \
    --bfile rawdata/pruned_v2.1 \
    --make-bed \
    --out resources/gwas

再用 R 语言脚本，用有表型数据的 resources/selected.fam 替换没表型数据的 resources/gwas.fam。（在替换的过程中，也对 ID 的顺序进行了校对）

library(tidyverse)

col_names <- c("FID", "IID", "Father", "Mother", "Sex", "Value")

empty_fam <- read_delim("resources/gwas.fam", col_names = col_names, delim = " ")
selected_fam <- read_delim("resources/selected.fam", col_names = col_names, delim = " ")

sorted_values <- selected_fam$Value[match(empty_fam$IID, selected_fam$IID)]

sorted_fam <- empty_fam %>%
    mutate(Value = sorted_values)

write_delim(sorted_fam, "resources/gwas.fam", delim = " ", col_names = F)

这样，用于 GWAS 的表型数据和基因型数据就准备好了。

PCA

理论上，并不是随便挑一些品种，测测表型就能够做 GWAS 的，如果品种间存在复杂的群体结构， GWAS 的结果很可能就有错误。我们可以通过绘制 PCA 图，来观察品种之间的关系。

首先用 PLINK，计算绘制 PCA 图所需的 EigenValue 和 EigenVector。

plink \
    --bfile resources/gwas \
    --pca \
    --out resources/pca_matrix

这将生成两个文件： resources/pca_matrix.eigenval 和 resources/pca_matrix.eigenvec。将生成的文件读入 R 中，用 ggplot 绘制 PCA 图（生成的文件为 results/pca.pdf）。

library(tidyverse)

eigenval <- scan("resources/pca_matrix.eigenval")
eigenvec <- read_delim(
    "resources/pca_matrix.eigenvec",
    col_names = c("FID", "IID", paste0("PC", 1:length(eigenval)))
)

pdf("results/pca.pdf")
ggplot(eigenvec) +
    geom_point(aes(x = PC1, y = PC2)) +
    labs(
        title = "PCA Plot",
        x = sprintf("PC1 Eigenvalue: %.2f", eigenval[1]),
        y = sprintf("PC2 Eigenvalue: %.2f", eigenval[2]),
    )
dev.off()

pca

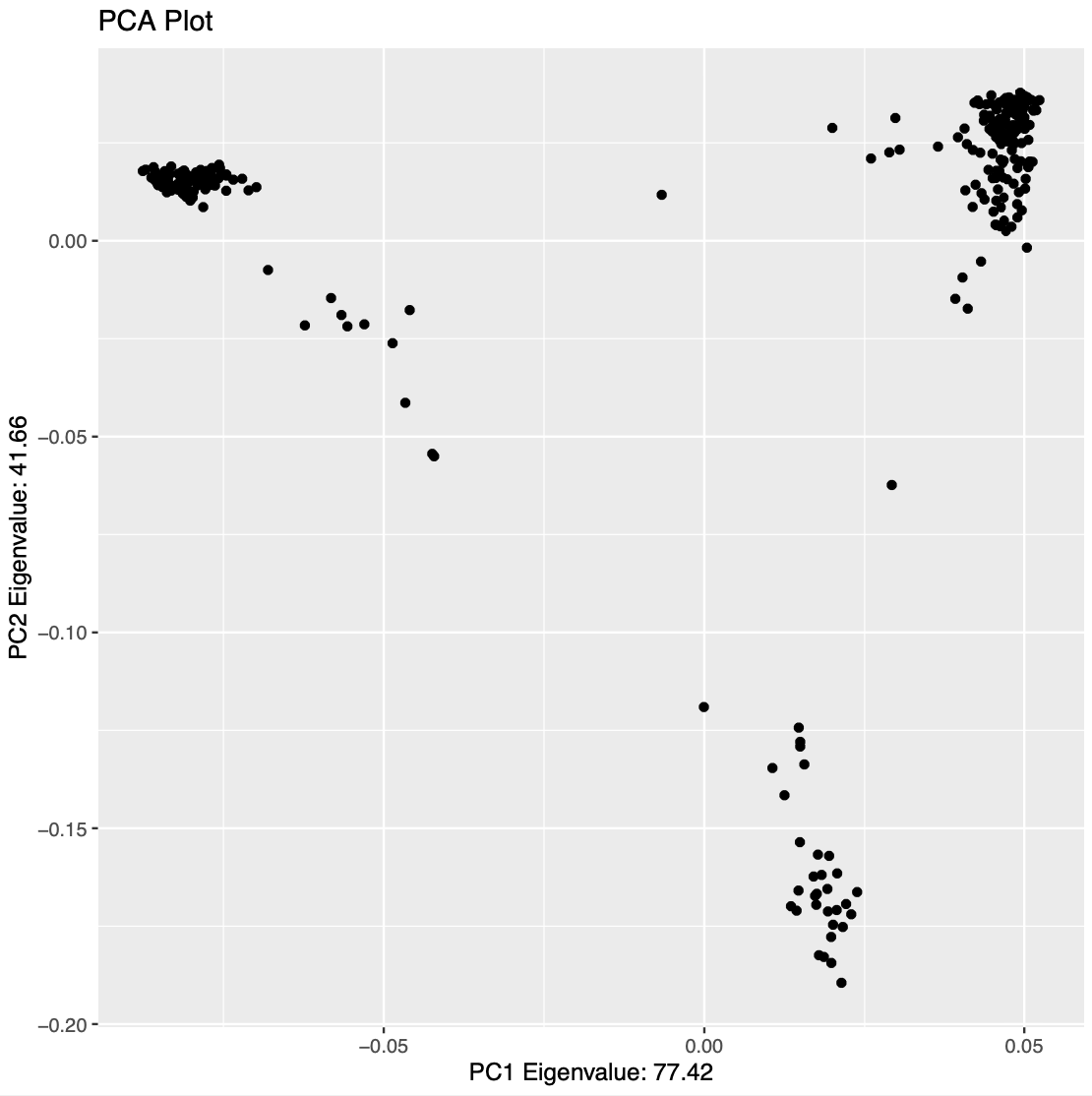
从图中可以看出，我们随机挑选的 300 个品种大致分成了三组，所以在后续的计算过程中，应对群体结构进行校正。

关联分析

我们选用 GEMMA 用来进行计算每个 SNP 与表型关联的 P 值。

详细的软件文档可在命令行中键入 gemma -h 或查阅在线文档。

首先，用 GEMMA 计算一个 300 个品种的亲缘矩阵，用以在后续的计算中矫正群体结构。

gemma \
    -bfile resources/gwas \
    -gk 1 \
    -outdir resources
    -o gemma_kinship

这将生成一个亲缘矩阵文件 resources/gemma_kinship.cXX.txt。

然后用 GEMMA 进行关联分析的计算。

gemma \
    -bfile resources/gwas \
    -k resources/gemma_kinship.cXX.txt \
    -lmm 1 \
    -outdir resources \
    -o gemma_gwa

这将生成一个较大的纯文本表格文件：resources/gemma_gwa.assoc.txt，内有 SNP 的相关信息，以及计算的 P 值。

Q-Q 图和曼哈顿图

虽然 GWAS 的大致原理就是对所有的 SNP 都进行关联分析，但实际上并不是一百万次 T 检验。

计算过程大概是这样的：先假设绝大多数 SNP 都与表型无实质关联，并用我们所提供的基因型和表型数据对模型的参数进行估计，使绝大多数 SNP 在这个模型里并没有与表型存在显著的关联，然后再把每个 SNP 都丢进这个模型里计算 P 值。这样存在“超乎寻常”的关联的 SNP 就会有一个“超乎寻常”的低的 P 值。

Q-Q 图可用于展示模型拟合的优良程度，而在曼哈顿图中，SNP 的 P 值越小，纵坐标就会越高，如果一个在一个较短的区域内有多个高度关联的 SNP，在曼哈顿图中就会形成一个关联的峰。

将之前计算所得的 resources/gemma_gwa.assoc.txt 读入 R，用 qqman 包即可绘制 Q-Q 图和曼哈顿图。

(生成 Q-Q 图文件：results/qq.pdf，生成的曼哈顿图文件：results/manhattan.pdf)

library(tidyverse)
library(qqman)

gwa_result <- read_tsv("resources/gemma_gwa.assoc.txt")

pdf("results/qq.pdf")
qq(gwa_result$p_wald)
dev.off()

pdf("results/manhattan.pdf")
manhattan(gwa_result, chr = "chr", bp = "ps", snp = "rs", p = "p_wald")
dev.off()

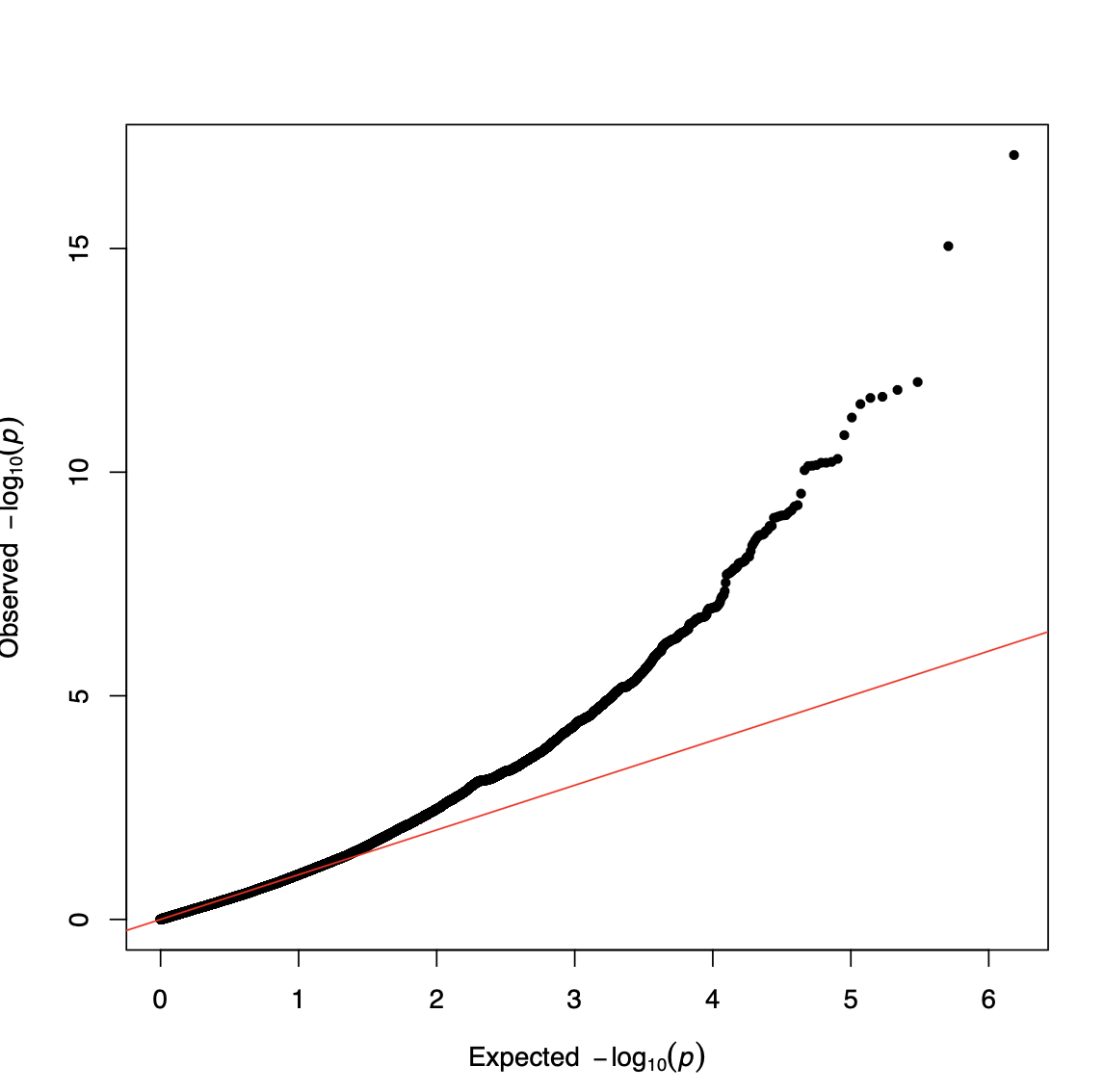
从 Q-Q 图中可以看出，大多数的 SNP 的 P 值都偏高，所以理论上关联分析的结果中将存在很多假阳性。

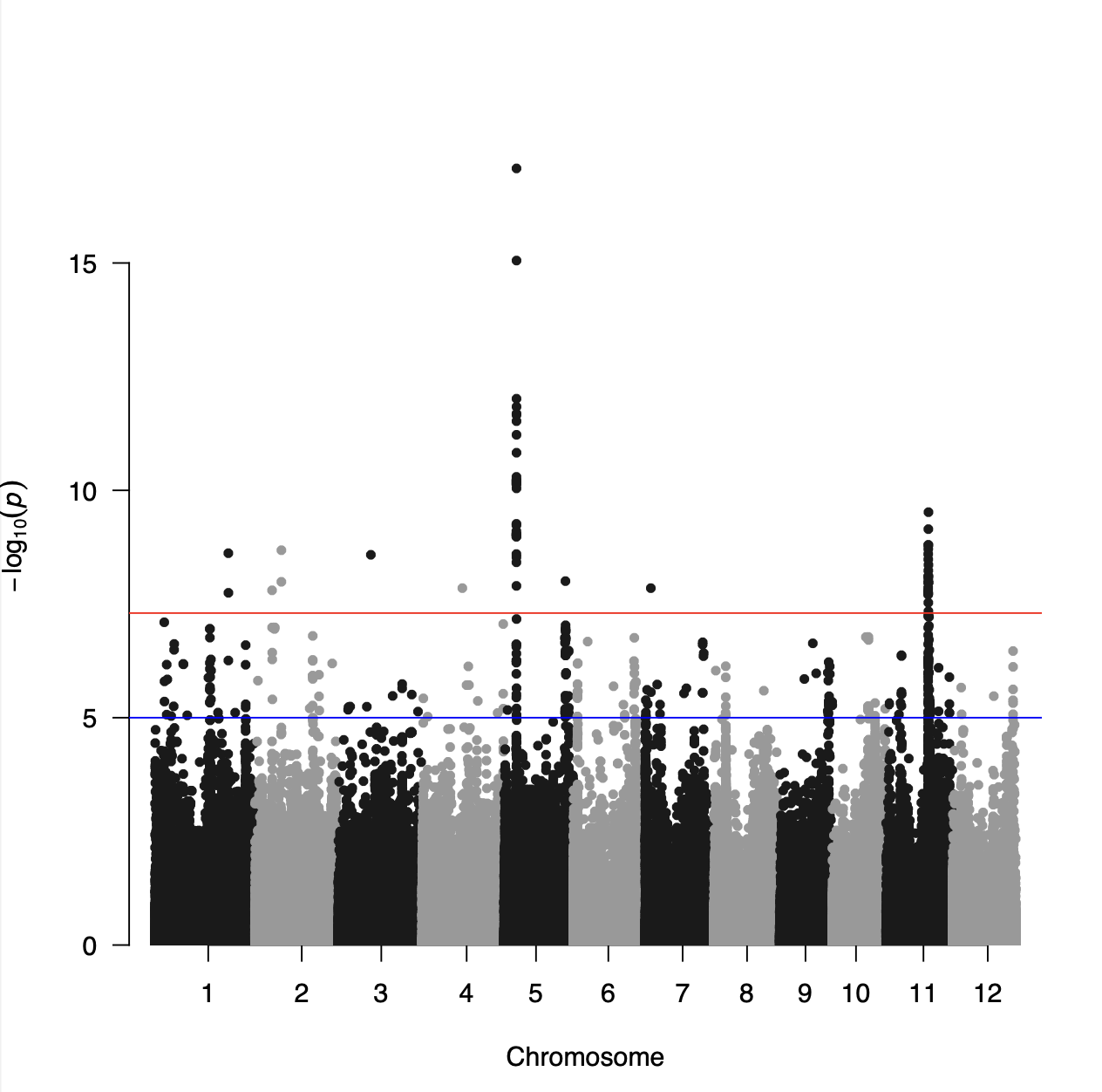
manhattan

从曼哈顿图中可以看出，5 号染色体上存在一个非常强的关联信号，我们可以用 R 脚本进一步查询 P 值最小的 SNP 的物理位置。

top10 <- function(chrom) {
    gwa_result %>%
        mutate(ps = as.character(ps)) %>%
        filter(chr == chrom) %>%
        arrange(p_wald) %>%
        select(chr, ps, p_wald, allele0, allele1) %>%
        slice_head(n = 10)
}

> top10(5)
# A tibble: 10 × 5
     chr ps        p_wald allele0 allele1
   <dbl> <chr>      <dbl> <chr>   <chr>
   5 5371949 8.11e-18 C       G
   5 5376161 8.84e-16 A       G
   5 5365256 9.67e-13 G       A
   5 5376243 1.45e-12 T       A
   5 5367026 2.06e-12 T       A
   5 5369058 2.19e-12 A       G
   5 5369111 3.01e-12 T       A
   5 5371214 6.01e-12 A       G
   5 5376245 1.49e-11 G       A
   5 5346621 5.05e-11 A       G

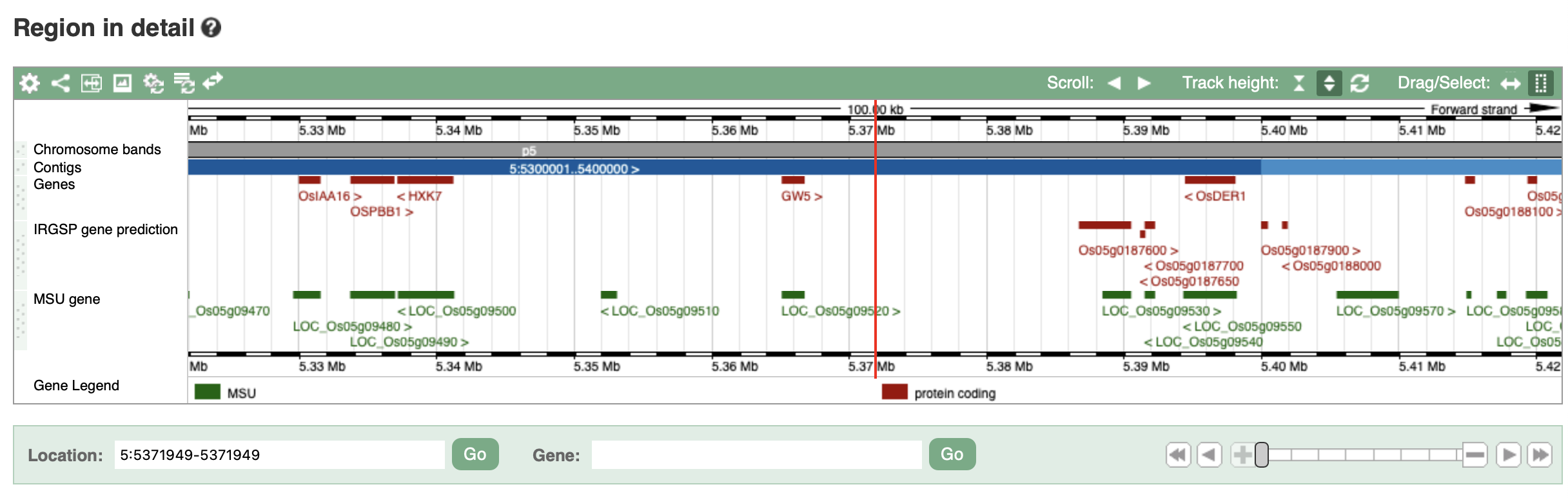
通过查询 5:5371949 位置的 SNP 附近的基因，不难发现，一个已知的控制粒宽的知名基因 —— GW5 就位于这个 GWAS 信号的附近。

ensembl-plant-genome-browser